註:本文同步更新在Notion!(數學公式會比較好閱讀)
最佳化理論(Optimization Theory)用來尋找數學問題中最優解。這些問題通常是指在某些條件下,尋找能使特定目標函數達到最大或最小值的解。最佳化理論讓算法能夠高效學習和調整模型的參數。
一個典型的最佳化問題可以表述為: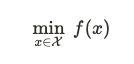 或
或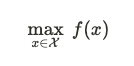
其中:
無約束最佳化
在無約束最佳化中,我們只需找到使目標函數達到最優值的參數 x,不需要考慮額外的條件或限制。
例子:最小化損失函數f(x),這在機器學習中的模型訓練過程中很常見。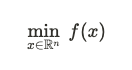
有約束最佳化
有約束最佳化會在參數 $x$ 上施加一組額外的條件,這些約束可以是等式或不等式的形式。
例子:Lagrange 乘數法常用來解決有約束的最佳化問題。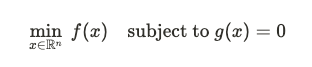
在機器學習中,梯度下降法是一種常用的無約束最佳化算法,用來尋找目標函數的最小值。它基於一個簡單的觀察:目標函數的梯度(導數)指向函數值增加最快的方向,因此我們沿著相反方向移動,以逐步逼近最小值。
梯度下降的公式
對於每次迭代,參數 x 根據梯度更新:
機器學習中的損失函數最小化
在訓練機器學習模型時,通常需要最小化損失函數(如均方誤差、交叉熵等)。梯度下降法會根據損失函數的梯度來調整模型參數,使得損失逐步減小,最終找到最佳參數組合。
牛頓法是一種迭代優化算法,利用了目標函數的二階導數(Hessian 矩陣)來加速收斂,特別適合求解凸函數的最優解。
Logistic Regression
在邏輯迴歸(Logistic Regression)的參數估計中,牛頓法是一種有效的優化方法,用來快速找到最大似然估計的解。
當最佳化問題存在約束條件時,拉格朗日乘數法是一種常用的工具。它通過引入拉格朗日乘數將有約束的問題轉化為無約束的問題。
拉格朗日函數:

通過求解拉格朗日方程,我們可以同時找到滿足約束條件且使目標函數達到最優的參數 x 和 λ 。
凸最佳化是最佳化理論中的一個特別重要的分支,因為凸函數的全局最小值是唯一的,這使得凸最佳化問題具有良好的數學性質和高效的解法。
凸函數的定義:

凸最佳化在機器學習中的應用
許多機器學習問題,如支持向量機(SVM)和正則化線性回歸,可以被表述為凸最佳化問題。這使得我們能夠利用凸最佳化技術來找到模型的全局最優解。
